Τα αρχαία Αιγυπτιακά Μαθηματικά

Οι απαρχές της γεωμετρίας

Η επιστήμη της γεωμετρίας (μέτρηση της γης) γεννήθηκε περί το 1.500 πΧ, για πρακτικούς λόγους, στην αρχαία Αίγυπτο, από όπου μεταδόθηκε αργότερα στην Ελλάδα, όπου και απογειώθηκε. Όλοι οι αρχαίοι Έλληνες ιστορικοί αναφέρονται στη σοφία των Αιγυπτίων ιερέων.

Οι συχνές πλημμύρες του Νείλου εξαφά-νιζαν τα όρια των ιδιοκτησιών και δημι-ουργούσαν την ανάγκη της συνεχούς κα-ταμέτρησης της γης, κάτι που έδινε πα-ράλληλα και τη δυνατότητα μιας δίκαιης κατανομής των φόρων, ανάλογα με την καλλιεργήσιμη έκταση του καθενός.

Η καταμέτρηση της έκτασης (εμβαδόν) των ιδιοκτησιών ήταν έργο των γραφέων (που υπάρχουν ήδη από την 3η χιλιετία πΧ), των αρπεδοναπτών και εν γένει κατάλληλα εκπαιδευμένων δημοσίων υπαλλήλων, απαλλαγμένων από άλλες εργασίες (με ελεύθερο χρόνο). 

Στην τοιχογραφία επάνω αρπενοδάπτης με τους βοηθούς του, επί το έργον. Η αρπεδόνη ήταν ένα μακρύ σκοινί με κόμπους, που απείχαν μεταξύ τους έναν πήχη. Το μήκος της ήταν ένα κετ = 100 πήχεις.

Αριστερά 

αγαλματίδιο του βασιλικού γραφέα Ραχοτέπ (2465-2350 π.Χ.), στο Εθνικό Αρχαιολογικό Μουσείο της Αθήνας 

και δεξιά 

ο καθιστός γραφέας της Σακάρα (2.600-2350 πΧ), που βρίσκεται σήμερα στο Λούβρο.

Πηγές

Η περίφημη στήλη της Ροζέττας, με εγχάρακτο κείμενο του 196 πΧ, που ανακαλύφθηκε τυχαία στην πόλη Rachid της κάτω Αιγύπτου, το 1799 μΧ, γραμμένο σε τρεις γραφές (ιερογλυφικά, δημώδη αιγυπτιακή και ελληνική), που συνέβαλλε αποφασιστικά στην αποκρυπτογράφηση των αιγυπτιακών ιερογλυφικών.

Σήμερα φυλάσσεται στο Βρετανικό Μουσείο.

Οι πηγές που διαθέτουμε σήμερα για τα αρχαία αιγυπτιακά μαθηματικά, είναι 12 πρωτότυπα κείμενα, από το 1850 πΧ ως το 750 μΧ, γραμμένα σε ιερογλυφική ή ιερατική γραφή, από δεξιά προς τα αριστερά. Κυριότερες:0 ο πάπυρος του Rhind, ο πάπυρος της Μόσχας, ο ΄δερμάτινος κύλινδρος' (1650 πΧ), σε ιερατική γραφή, σήμερα στο Βρετανικό Μουσείο,  όπως και ο 'πάπυρος Καχούν' και τέλος ο 'πάπυρος 6619 του Βερολίνου'.

Ο μαθηματικός πάπυρος του Ρίντ

Ο περίφημος πάπυρος του Αχμές (αντίγραφο του 1855 πΧ, ενός παλαιότερου κατά 200 χρόνια), γραμμένος στην ιερατική γραφή. Βρέθηκε στην αρχαία πόλη των Θηβών (το 1830) και περιέχει 84 μαθηματικά προβλή-ματα με τις απαντήσεις τους. 

Είναι γνωστός και ως 'πάπυρος του Rhind'. Σήμερα στο Βρετανικό Μουσείο και στο Μουσείο Μπρούκλιν.

Περιέχει τον πρώτο μαθηματικό γρίφο της Ιστορίας: 'Επτά σπίτια έχουν το καθένα επτά γάτες, η καθεμιά από τις οποίες τρώει επτά ποντίκια, που έφαγαν επτά σπόρους σιταριού το καθένα, ενώ ο κάθε σπόρος θα είχε παραγάγει 35 κιλά αλεύρι'. Η απάντηση του δυσεπίλυτου αινίγματος είναι 19.607.

Ο πάπυρος του Βερολίνου

Πρόκειται για ένα κείμενο του 1300 πΧ, στο οποίο κάποιοι ισχυρίζονται ότι οι Αιγύπτιοι λύνουν εξισώσεις β΄ βαθμού, όπως αυτή: να βρεθούν δυο ποσότητες που το άθροισμα τους είναι 14 και το γινόμενο τους 48. Σήμερα θα λέγαμε:
x+ψ = 14 και xψ = 48.

Εξαιρετικά σημαντικός, αφού περιέχει όμως και την πρώτη γνωστή κατα-γραφή διάγνωσης εγκυμοσύνης.

    

Ο πάπυρος της Μόσχας

γνωστός και ως πάπυρος του Γκολενίστσεφ (αριστερά), που τον αγόρασε από τις Θήβες και τον πούλησε στο Κρατικό Μουσείο Καλών Τεχνών Πούσκιν (δεξιά), όπου βρίσκεται μέχρι σήμερα. 

Έχει μήκος 5,5 μ. και πλάτος 3,8-7,6 εκατοστά και περιέχει 25 μαθηματικά προβλήματα, που μελέτησε ο Σοβιετικός ασιανολόγος Βασίλι Στρούβε, το 1930.

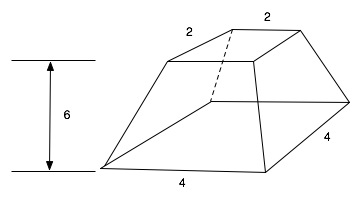Ένα πρόβλημα (το 10) θεωρείται ότι είναι ιδιαίτερης σημασίας, επειδή δίνει μία μέθοδο για την εύρεση του όγκου μιας κόλουρης πυραμίδας {V=h/3(a²  + ab + b²)}:

'Σας λένε ότι μια κόλουρη πυραμίδα έχει ύψος 6, μήκος 4 στη βάση και 2 στην κορυφή. 

Υψώνετε το 4 στο τετράγωνο, αποτέλεσμα 16. Διπλασιάζετε το 4 αποτέλεσμα 8. Υψώνετε στο τετράγωνο αυτό το 2, αποτέλεσμα 4. Προσθέτετε το 16 και το 8 και το 4, αποτέλεσμα 28. Παίρνετε το 1/3 του 6, αποτέλεσμα 2. Παίρνετε το 28 δυο φορές, αποτέλεσμα 56. Βλέπετε, είναι 56. Θα βρείτε ότι είναι σωστό'.

σύστημα αρίθμησης

Το σύστημα τους είναι δεκαδικό, αλλά μη θεσιακό.

Το τρία πχ σχηματίζεται με τρεις επαναλή-ψεις της μονάδας,

ενώ το τριάντα, όπως και στο ρωμαϊκό σύστημα, με τρεις επαναλήψεις του 10.

αριθμητική

Η θεμελιώδης πράξη είναι η πρόσθεση. Σε αυτήν ανάγονται ο πολλαπλασιασμός (μέσω διαδοχικών διπλασιασμών) και η διαίρεση (με υποδιπλασιασμούς: 1/2, 1/4, 1/8 κλπ).

Οι Αιγύπτιοι χρησιμοποιούν τα εναδικά κλάσματα (με αριθμητή τη μονάδα: 1/η , με μοναδική εξαίρεση το κλάσμα 2/3), αλλά δεν τα προσθέτουν. Πχ η διαίρεση 19:8 δίνει το μικτό αποτέλεσμα 2 1/4/1/8 και όχι 2 3/8 .

Οι υπολογισμοί ΄αχά΄

Ουσιαστικά έχουμε αυτό που σήμερα θα λέγαμε επίλυση αλγεβρικών προβλημάτων α΄ βαθμού με έναν άγνωστο (x). Εδώ ο άγνωστος αναφέρεται ως 'αχά', που σημαίνει σωρός ή ποσότητα και η λύση γίνεται με την υπολογιστική μέθοδο της 'αυθαίρετης παραδοχής' (method of faulse position), που διδασκόταν στα σχολεία της Ευρώπης και της Αμερικής ως και τον 19ο αι.

Παράδειγμα το πρόβλημα 40 ή το 26 του Rhind, όπου ζητείται να υπολογιστεί μια ποσότητα, που μαζί με το τέταρτο της κάνει 15. Σήμερα θα λέγαμε: x + x/4 = 15

Οι αρχαίοι Αιγύπτιοι το έλυναν με δοκιμές:  Επιλέγουμε αυθαίρετα έναν αριθμό σαν πιθανή λύση, μικρότερο βέβαια του 15 (και πολλαπλάσιο του 4, για να έχουμε ακέραιες λύσεις). Έστω πχ ότι το ζητούμενο είναι ο αριθμός 8. Το τέταρτο του (x/4) είναι 2, άρα το άθροισμα τους 10, μικρότερο του 15 (λάθος). Αλλάζουμε αυθαίρετη τιμή (ανεβαίνουμε) στο 12, που το τέταρτο του είναι 3, άρα το άθροισμα τους 15 (σωστό).

Επίλογος

Όλα τα μαθηματικά προβλήματα που βρέθηκαν σε αιγυπτιακά κείμενα αφορούν πρακτικές εφαρμο-γές. Πουθενά δεν είναι ζητούμενο να κατασκευασθεί ή να αποδειχθεί κάτι. Υπάρχουν βέβαια αρκετά θεωρητικά, μη ωφελιμιστικά  προβλήματα,  επινοημένα για τις ανάγκες της εκπαίδευσης των νέων γραφέων, με κάποιο βαθμό αφαίρεσης, αλλά αυτό απέχει πολύ από την αποδεικτική μέθοδο των ελλήνων γεωμετρών.