Η προϊστορία της πληροφορικής

το όνειρο του Λάιμπνιτζ

   

Gottfried Wilhem Leibnitz 

(1646-1716)

Ο σπουδαίος Γερμανός φιλόσοφος και μαθηματικός Λάιμπντιτς, σύγχρονος του Νεύτωνα, ο 'πολυμαθέστερος άντρας μετά τον Αριστοτέλη', εκφράζει από τον 17ο ήδη αιώνα (1678), τη φιλόδοξη ιδέα μιας παγκόσμιας γλώσσας (characteristica universalis). 

Μια τυπική, συμβολική γλώσσα, που θα μπορούσε να εκφράσει την ανθρώπινη σκέψη, με ακρίβεια και συνέπεια,  με μια γενική συμβολική μέθοδο, που θα είχε τη δυνατότητα της αναγωγής κάθε αλήθειας σε ένα είδος μαθηματικού υπολογισμού. Φανταστείτε την σαν ένα αλφαβητάριο της ανθρώπινης σκέψης, μια άλγεβρα της σκέψης, που ο κάθε λαός θα μπορούσε να αντιληφθεί και να μεταφράσει στη γλώσσα του εύκολα και χωρίς λεξικό, μέσω της οποίας θα μπορούσαν όλες οι επιστημονικές και φιλοσοφικές διερευνήσεις να αναχθούν σε απλούς υπολογισμούς. Κάθε νοητικό σφάλμα θα απεικονίζεται ως υπολογιστικό σφάλμα. 

Η αισιοδοξία του ήταν τέτοια που δήλωνε πως θα αρκούσαν για το εγχείρημα αυτό 'πέντε μόνον χρόνια και μερικοί σωστά επιλεγμένοι άντρες'. Επινόησε μια σειρά από μαθηματικά σύμβολα, χρησιμοποίησε σαν βάση τη γερμανική γλώσσα, εμπλουτισμένη με κάποια άλλα σύμβολα, εμπνευσμένα από τα κινέζικα και αιγυπτιακά ιερογλυφικά ή και τα σύμβολα της αλχημείας, σύμβολα από τις νότες της μουσικής, που καταργούν τις λέξεις και λειτουργούν όπως τα σύμβολα των αριθμών στην άλγεβρα, παριστάνουν δηλαδή έννοιες αντί για λέξεις-ήχους.

Κάποια από τα βασικά ιδεογράμματα του Λάιμπνιτς

Bernard Bolzano
(1781-1848)

Το εγχείρημα του δεν βρήκε άξιους συνεχιστές στην εποχή του. Μοναδική εξαίρεση αποτελεί ο Μ. Μπολζάνο, που ανέπτυξε κεντρικές  έννοιες της μαθηματικής (μορφικής) λογικής (η επιστήμη των νόμων της σκέψης), όπως η λογική συνέπεια, χρησιμοποιώντας μια εν μέρει τυπική γλώσσα: σαν βάση είχε τα σύμβολα της γερμανικής γλώσσας, εμπλουτισμένη όμως και με άλλα σύμβολα για τις σταθερές και τις μεταβλητές του.  

Ο Λάιμπνιτζ, που χαρακτηρίστηκε ως το καθολικό πνεύμα της εποχής του (homo universalis), δεν βρήκε τον χρόνο να ασχοληθεί περισσότερο με την ιδέα του αυτή. Παρέμεινε έτσι στο ράφι' για δυο περίπου αιώνες, μέχρι να την ανασύρει ένας άλλος σπουδαίος μαθηματικός, ο Μπουλ και να της δώσει σάρκα και οστά. 

Ο Άγγλος μαθηματικός George Boole (1815-1864), είναι αυτός που συνέβαλε καθοριστικά στη διαμόρφωση της ανεξάρτητης επιστήμης της συμβολικής λογικής (1847), γνωστής σήμερα ως άλγεβρα Μπουλ, στην οποία στηρίχθηκε η σχεδίαση των ψηφιακών ηλεκτρονικών υπολογιστών, η δημιουργία 'λογιστικού λογισμού'. Η δυαδική (ή διακοπτική) άλγεβρά του, είναι μια σαφής δίτιμη λογική, με δυο μόνον στοιχεία, 'λογικές μετα-βλητές': το Ο και το 1, που  αντιπροσωπεύουν τις αριστοτελικές αληθο-τιμές: 'αληθές' και ΄ψευδές'.  Πρόκειται για την πρώτη μορφή προτασια-κού λογισμού, που ανάγει τις λογικές διαδικασίες σε  μαθηματικά επεξερ-γάσιμες προτάσεις.

Οι σημαντικότερες εργασίες του είναι η: Μαθηματική Ανάλυση της Λογικής¨ (Mathematical Analysis of Logic, 1847) και οι ¨Νόμοι της Σκέψης", 1854.

Σε αντίθεση με την ασαφή γλώσσα της ποίησης, της λογοτεχνίας και της φυσικής γλώσσας. που στηρίζονται σε μια πλειότιμη ασαφή λογική, με άπειρες διαβαθμίσεις μεταξύ του 0 και του 1, η άλγεβρα του Μπουλ είναι μεν απόλυτα σαφής, αλλά  φτωχή σε δυνατότητες. Σε συμβολικό επίπεδο, το 0 και το 1, σύμφωνα με τον Λακάν παριστάνουν το παιχνίδι παρουσίας-απουσίας.

Το πρόγραμμα αναλαμβάνουν να ολοκληρώσουν δυο κορυφαίοι μαθηματικοί και φιλόσοφοι, της λογικιστικής σχολής: ο Γερμανός Γκότλομπ Φρέγκε, ένας από τους ιδρυτές της σύγχρονης μη αριστοτελικής λογικής (μελέτη της διασύνδεσης μεταξύ των ισχυρισμών, που οδηγούν σε ένα συμπέρασμα, ανάλυση και έλεγχος της ορθότητάς του), που εισήγαγε τη διάκριση μεταξύ αναφοράς (μιας έκφρασης) και του νοήματός της, αλλά και εισηγητής της αναλυτικής φιλοσοφίας (γλωσσική στροφή της φιλοσοφίας, που δυσπιστεί στην καθημερινή φυσική γλώσσα, με κορυφαίο εκπρόσωπό της τον Βιτγκενστάιν ) και ο Άγγλος μαθηματικός, αλλά και λογοτέχνης Μπέρντραντ Ράσελ (Νόμπελ Λογοτεχνίας το 1950), ένας από τους  μεγαλύτερους λογικούς φιλοσόφους μετά τον Αριστοτέλη.

                                                                                                                            

Gottlob Frege     
(1848-1925)                                                                                                 
Την ιδέα του προχώρησε ο Φρέγκε, με ένα φιλόδοξο ερευνητικό πρόγραμμα, που προσπάθησε να επαναθεμελιώσει τα μαθηματικά (κυρίως την αριθμητική) στη λογική. 

Στην Εννοιογραφία του (Begriffsschrift), προσπαθεί να δείξει ότι μέρη της αριθμητικής (όπως η Ανάλυση και η Θεωρία των Αριθμών) είναι μέρη της λογικής, ενώ για τη γεωμετρία υποστηρίζει πως αρκεί μια ιδιότητα, για να περιγράψει το σύνολο των αντικειμένων που την ικανοποιούν.

Bertrand Russell

(1872-1970)

Τα αδιέξοδα του προγράμματος, τις λογικές αντινομίες του (όπως το 'παράδοξο του κουρέα', 1901), θα επισημάνει ο κορυφαίος Άγγλος μαθηματικός, θεμελιωτής της αναλυτικής φιλοσοφίας, ειρηνιστής και Νομπελίστας λογοτέχνης B. Russel, στο τρίτομο έργο του Οι Αρχές των Μαθηματικών (Prncipia Mathematica, που έγραψε σε συνεργασία με τον Alfred Whitehead), εμπνευσμένο από τα Στοιχεία του Ευκλείδη. Εκεί αναπτύσσουν τη λεγόμενη 'θεωρία των τύπων' και καταφέρνουν να ξεπεράσουν τον σκόπελο των παραδόξων, με την 'αρχή του φαύλου κύκλου', σύμφωνα με την οποία δεν μπορούμε να ορίσουμε κάτι με αναφορά σε ένα σύνολο που το περιέχει.

Θα συνεχίσει παρ΄όλα αυτά την προσπάθεια, διατηρώντας την πίστη του στη δυνατότητα αναγωγής των μαθηματικών στη λογική. Το πρόγραμμα του συνεχίζει ο Χίλμπερτ, διερευνώντας τη δυνατότητα δημιουργίας ενός συνόλου αξιωμάτων, ικανό για όλα τα μαθηματικά, μέχρι να έρθει ο νεαρός Γκέντελ και να δώσει,  το 1931, το τελειωτικό χτύπημα στις επίμονες προσπάθειες μισού αιώνα,  δείχνοντας πως είναι αδύνατον να κατασκευαστεί ένα πλήρες και συνεπές σύστημα από αξιώματα,για όλα τα μαθηματικά.

Kurt Godel
(1906-1978)
Ο κορυφαίος λογικός του 20ου αι., (τενός φίλος του Αϊνστάιν στο Πρίνστον), που απέδειξε  (σε ηλικία 25 μόλις ετών, ένα χρόνο μετά την απόκτηση του διδακτορικού του από το Παν/μιο της Βιέννης), δυο από τα θεμελιώδη σύγχρονα θεωρήματα της φιλοσοφίας των μαθηματικών: το "θεώρημα της πληρότητας του κατηγορηματικού λογισμού α΄ βαθμού" και το "θεώρημα μη πληρότητας της τυπικής αριθμητικής".

Μια από τις συνέπειες των θεωρημάτων του είναι και ότι δεν είναι δυνατόν να απαντηθούν όλες οι ερωτήσεις των μαθηματικών.


Ο ΄δικός μας΄ ο Δ. Νανόπουλος θα δηλώσει σε συνέντευξή του ότι τα θεωρήματα του Γκέντελ είναι προφανώς ισοδύναμα  με την αρχή της αβεβαιότητας του Χάιζενμπεργκ και είναι περίεργο που κανείς δεν το έχει επισημάνει ως τώρα.

Stephen Cole Kleene

Ο Αμερικανός μαθηματικός Στήβεν Κλέινι, (ιδρυτής της θεωρίας της αναδρομής), έδειξε το 1943, ότι μια από τις συνέπειες της μη πληρότητας (του Γκέντελ), είναι και η μη υπολογισιμότητα στην Eπιστήμη των Υπολογιστών. 

Το 'πρόβλημα του τερματισμού' δεν έχει λύση, είναι μη αποφασίσιμο. 

Δεν υπάρχει δηλαδή πρόγραμμα υπολογιστή που δοθέντος ενός προγράμ-ματος Π ως είσοδο, να μπορεί να αποφασίσει σωστά αν το Π σταματά τελικά, όταν τρέξει χωρίς είσοδο.

Είκοσι χρόνια αργότερα (το 1963) ο Paul Cohen θα αποδείξει ότι το 'αξίωμα επιλογής' και η 'υπόθεση του συνεχούς' στη Θεωρία των Συνόλων, είναι προτάσεις ανεξάρτητες από τα συνήθη αξιώματα της θεωρίας αυτής.

από την προϊστορία 
στην ιστορία της πληροφορικής

Η αποτυχία του φιλόδοξου ερευνητικού προγράμματος για την κατασκευή μιας παγκόσμιας γλώσσας, με την αντικατάσταση της φυσικής μας γλώσσας από μια κατασκευασμένη τυπική γλώσσα, χωρίς αμφισημίες και λογικές αντιφάσεις, κάθε άλλο παρά άγονη ήταν. Ο σκοπός μπορεί να μην επετεύχθη, το όραμα του Λάιμπνιτς δεν έγινε πραγματικότητα, αλλά ο δρόμος που άνοιξε ήταν απίστευτα δημιουργικός, αφού οδήγησε στην εποχή των ηλεκτρονικών υπολογιστών.

Θα κλείσουμε το άρθρο, με μια σύντομη αναφορά σtον  άνθρωπο που είδε τη δυνατότητα κατασκευής μιας σύγχρονης ηλεκτρικής υπολογιστικής μηχανής, που δεν είναι άλλος από τον:

Claude Shannon 

(1916-2001)

Ένας ιδιοφυής Αμερικανός μαθηματικός και ηλεκτρολόγος μηχανι-κός, ο άνθρωπος που απέδειξε ότι με ένα απλό ηλεκτρονικό κύκλωμα, με λυχνίες και διακόπτες, μπορούμε να πούμε αν μια λογική πρόταση είναι αληθής ή ψευδής. Καθηγητής στο ΜΙΤ, μέλος μεταξύ άλλων, της Αμερικανικής Φιλοσοφικής Ακαδημίας και της Εθνικής Ακαδημίας Επιστημών των ΗΠΑ, γνωστός και ως "πατέρας  της ψηφιακής επικοινωνίας", ο άνθρωπος που έθεσε τα θεμέλια για τα σύγχρονα τηλεπικοινωνιακά δίκτυα. Είναι αυτός που ανέδειξε την πληροφορία σε μετρήσιμο και αυστηρά ορισμένο μέγεθος, που θα μπορούσε να χειριστεί ακόμη και μια μηχανή.

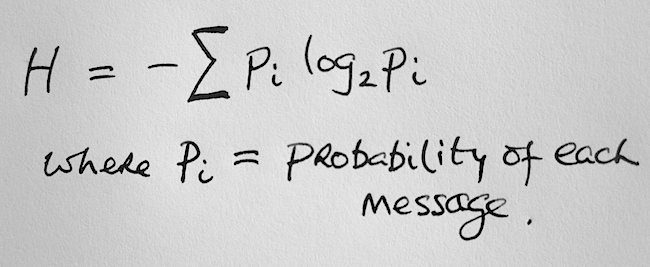Μεγάλη ήταν η συνεισφορά του και στην ανάπτυξη των Η/Υ, αφού πρώτος έδειξε ότι με βάση την άλγεβρα Boole (1854) είναι δυνατή η δημιουργία ψηφιακών ηλεκτρικών κυκλωμάτων, για την επίλυ-ση μαθηματικών εξισώσεων. 


Η βασική του ιδέα, που παρουσίασε στη διατριβή του A Symbolic Analysis of Lelay and Switching Circuits, είναι πως με κατάλληλες συνδεσμολογίες διακοπτών είναι δυνατή η κατασκευή των τριών θεμελιωδών λογικών πυλών: NOT (για την άρνηση ή αντιστροφή), OR (για τη διάζευξη) και AND (για τη σύζευξη). Είναι ο πρώτος που οραματίστηκε μια επικοινωνία σε δυαδικό κώδικα, ο οποίος θα μπορούσε να συμβολίζει οτιδήποτε: λέξεις, ήχους (μουσική), εικόνες, ακόμη και (γιατί όχι ;) ιδέες.

Κατά την παραμονή του στο ΜΙΤ ορίστηκε υπεύθυνος για τη λειτουργία του Διαφορικού Αναλυτή (Differential Analyzer), ο οποίος ήταν ένας υπολογιστής αποτελούμενος από μηχανικά μέρη και χρησίμευε για την επίλυση σύνθετων εξισώσεων. Γρήγορα άρχισε να σκέφτεται τρόπους βελτί-ωσης του Διαφορικού Αναλυτή με τη χρήση ηλεκτρικών κυκλωμάτων στη θέση των δύσχρηστων μηχανικών μερών.

Από το 1941 μετέχει σε ερευνητική ομάδα της Bell Telephone, που εργάζεται σε πρόγραμμα βελτίωσης της αξιοπιστίας των υπεραστικών τηλεφωνικών και τηλεγρα-φικών επικοινωνιών και αναπτύσσει πιο αποτελεσματικές μεθόδους μετάδοσης και αποθήκευσης της πληροφορίας. Θεωρείται ''πατέρας της σύγχρονης κρυπτολογίας" (ας μην ξεχνάμε ότι βρισκόμαστε στην καρδιά του Β΄ Παγκόσμιου Πόλεμου και η ανάγκη αποκρυπτογράφησης των γερμανικών μηνυμάτων είναι για τους συμμάχους τεράστιας σημασίας). 

Η "Μαθηματική Θεωρία της Επικοινωνίας", των Shannon-Weaver.

Μια πρωτοποριακή και επαναστατική εργασία, που εισάγει το ποσοτικό αλλά και ποιοτικό μοντέλο επικοινωνίας, που στηρίζεται στη θεωρία της πληροφορίας.

Δημιουργήθηκε το 1944 στα εργαστήρια της Bell και δημοσιεύτηκε το 1948.

  

"το θεμελιώδες πρόβλημα της επικοινωνίας είναι η αναπαραγωγή σε ένα σημείο, 

είτε ακριβώς είτε κατά προσέγγιση, ενός μηνύματος που επιλέχτηκε σε ένα άλλο σημείο"

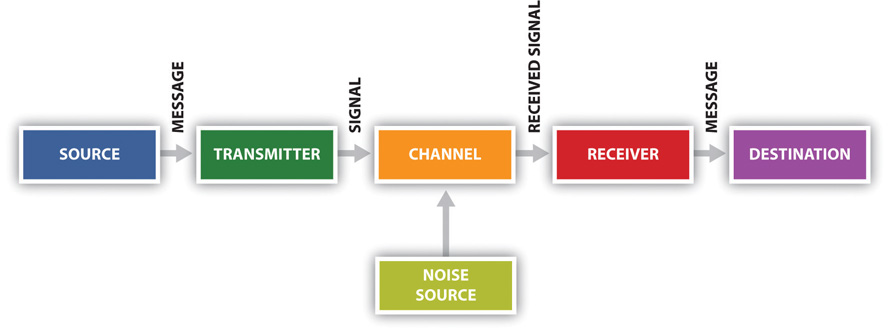
To μοντέλο επικοινωνίας των Shannon-Weaver

(για ραδιόφωνο, ΤV, τηλέφωνο κλπ)

Η πηγή είναι ο χώρος όπου επιλέγεται η πληροφορία, το μήνυμα που θέλουμε να στείλουμε. Σε πρώτη φάση κωδικοποιείται και κατόπιν εκπέμπεται μέσα από ένα κανάλι, δίαυλο επικοινωνίας (που εισάγει αναπόφευκτα κάποιο θόρυβο, παράσιτα) μεταφέρεται σε ένα άλλο σημείο, όπου γίνεται αντιληπτό από τον δέκτη. Εκεί αποκωδικοποιείται και μεταφράζεται. Η επικοινωνία είναι επιτυχής στο μέτρο που η εικόνα που συνθέτει ο δέκτης, είναι εκείνη που θέλησε να στείλει ο πομπός.