Διευκρίνηση των απαραίτητων όρων
για να βάλουμε κάποια ... τάξη στο ... Χάος
Εισαγωγή
Χάος είναι η επιστήμη της πολυπλοκότητας, με σημαντικές εφαρμογές στη μετεωρολογία, την οικονομία, την πληροφορική, αλλά και τη φυσιολογία, τη μηχανική των ρευστών κ.α.
Πρόκειται για μια νέα επιστήμη, που αναπτύσσεται δυναμικά μετά την δεκαετία του 1960, με τη χρήση ηλεκτρονικών υπολογιστών, θέτοντας και αντιμετωπίζοντας νέα πολύπλοκα προβλήματα.
Πρωτοεμφανίζεται τη δεκαετία του 1880, όταν ο κορυφαίος Γάλλος μαθηματικός Henri Poincare μελετά τη σταθερότητα του ηλιακού μας συστήματος. Πρόκειται για το γνωστό ως 'πρόβλημα των τριών σωμάτων' με βαρυτική αλληλεπίδραση (Ήλιος, Γη, Σελήνη, αφήνοντας απέξω τις επιδράσεις από τους άλλους πλανήτες, αλλά και από γειτονικούς γαλαξίες) και συνειδητοποιεί πως είναι μη ολοκληρώσιμο, άρα δεν επιλύεται με μαθηματική ανάλυση (έχει επιλυθεί μόνον αριθμητικά, με τη βοήθεια ΗΥ, η επίλυση του είναι συγκλονιστικά πολύπλοκη) και ότι σε βάθος χρόνου οι τροχιές τους αποκλίνουν.
Θα περάσει ένας αιώνας μέχρι να κάνουν την εμφάνιση τους τα φράκταλ και μόνον το 1977 θα πραγματοποιηθεί από την Ακαδημία Επιστημών της Ν. Υόρκης, το πρώτο διεθνές συνέδριο για το χάος.
Είναι η στιγμή που κλονίζεται αναπάντεχα, από τα θεμέλια της, η σιγουριά της επιστήμης και φαίνεται πλέον καθαρά ότι η αισιοδοξία της νευτώνειας μηχανικής σκοντάφτει σε ανυπέρβλητα εμπόδια. Η πίστη για την απλότητα του σύμπαντος και τη δυνατότητα ασφαλούς περιγραφής και πρόβλεψης των μεταβολών του, δεν είναι παρά μια ανεφάρμοστη ουτοπία, μια όχι και τόσο απλή υπόθεση, ούτε και δεδομένη.
Μεγάλη συμβολή για την ανάπτυξη της νέας αυτής επιστήμης προήλθε από τους ηλεκτρονικούς υπολογιστές, από τη δεκαετία του 1960, αφού οι μη γραμμικές εξισώσεις που υπεισέρχονται στην μελέτη της πολυπλοκότητας μόνο με ισχυρή υπολογιστική δύναμη μπορούσαν ν’αντιμετωπιστούν (απαιτούν απίστευτα πολλούς υπολογισμούς, με συνεχή επανάληψη απλών μαθηματικών τύπων, που είναι αδύνατον να γίνουν με το χέρι).
Η ονομασία, Θεωρία του Χάους, δόθηκε το 1975, από τον Αμερικανό μαθηματικό Jim York, του Πανεπιστημίου του Maryland.
Συμπέρασμα
Το μέλλον δεν είναι σε καμία περίπτωση προκαθορισμένο. Παραμένει ανοικτό και ο δρόμος είναι γεμάτος με απροσδόκητες εκπλήξεις.
Αιτιοκρατία και ασφαλής πρόβλεψη δεν είναι το ίδιο πράγμα.
Που αναφέρεται
το χάος αναφέρεται σε ντετερμινιστικά, πολυδύναμα, μη διατηρητικά (ανοικτά), μη γραμμικά δυναμικά συστήματα, μακράν της θερμοδυναμικής ισορροπίας.
αφορά κάθε μη περιοδική, απρόβλεπτη (σε μακρά χρονική εξέλιξη) συμπεριφορά ενός ανοικτού συστήματος, που κάτω από ορισμένες συνθήκες, είναι ευαίσθητη στις αρχικές συνθήκες (συνθήκες εκκίνησης).
Χάος είναι η επιστήμη της πολυπλοκότητας, με σημαντικές εφαρμογές στη μετεωρολογία, την οικονομία, την πληροφορική, αλλά και τη φυσιολογία, τη μηχανική των ρευστών κ.α.
Πρόκειται για μια νέα επιστήμη, που αναπτύσσεται δυναμικά μετά την δεκαετία του 1960, με τη χρήση ηλεκτρονικών υπολογιστών, θέτοντας και αντιμετωπίζοντας νέα πολύπλοκα προβλήματα.
Πρωτοεμφανίζεται τη δεκαετία του 1880, όταν ο κορυφαίος Γάλλος μαθηματικός Henri Poincare μελετά τη σταθερότητα του ηλιακού μας συστήματος. Πρόκειται για το γνωστό ως 'πρόβλημα των τριών σωμάτων' με βαρυτική αλληλεπίδραση (Ήλιος, Γη, Σελήνη, αφήνοντας απέξω τις επιδράσεις από τους άλλους πλανήτες, αλλά και από γειτονικούς γαλαξίες) και συνειδητοποιεί πως είναι μη ολοκληρώσιμο, άρα δεν επιλύεται με μαθηματική ανάλυση (έχει επιλυθεί μόνον αριθμητικά, με τη βοήθεια ΗΥ, η επίλυση του είναι συγκλονιστικά πολύπλοκη) και ότι σε βάθος χρόνου οι τροχιές τους αποκλίνουν.
Είναι η στιγμή που κλονίζεται αναπάντεχα, από τα θεμέλια της, η σιγουριά της επιστήμης και φαίνεται πλέον καθαρά ότι η αισιοδοξία της νευτώνειας μηχανικής σκοντάφτει σε ανυπέρβλητα εμπόδια. Η πίστη για την απλότητα του σύμπαντος και τη δυνατότητα ασφαλούς περιγραφής και πρόβλεψης των μεταβολών του, δεν είναι παρά μια ανεφάρμοστη ουτοπία, μια όχι και τόσο απλή υπόθεση, ούτε και δεδομένη.
Μεγάλη συμβολή για την ανάπτυξη της νέας αυτής επιστήμης προήλθε από τους ηλεκτρονικούς υπολογιστές, από τη δεκαετία του 1960, αφού οι μη γραμμικές εξισώσεις που υπεισέρχονται στην μελέτη της πολυπλοκότητας μόνο με ισχυρή υπολογιστική δύναμη μπορούσαν ν’αντιμετωπιστούν (απαιτούν απίστευτα πολλούς υπολογισμούς, με συνεχή επανάληψη απλών μαθηματικών τύπων, που είναι αδύνατον να γίνουν με το χέρι).
Η ονομασία, Θεωρία του Χάους, δόθηκε το 1975, από τον Αμερικανό μαθηματικό Jim York, του Πανεπιστημίου του Maryland.
Συμπέρασμα
Το μέλλον δεν είναι σε καμία περίπτωση προκαθορισμένο. Παραμένει ανοικτό και ο δρόμος είναι γεμάτος με απροσδόκητες εκπλήξεις.
Αιτιοκρατία και ασφαλής πρόβλεψη δεν είναι το ίδιο πράγμα.
Που αναφέρεται
το χάος αναφέρεται σε ντετερμινιστικά, πολυδύναμα, μη διατηρητικά (ανοικτά), μη γραμμικά δυναμικά συστήματα, μακράν της θερμοδυναμικής ισορροπίας.
αφορά κάθε μη περιοδική, απρόβλεπτη (σε μακρά χρονική εξέλιξη) συμπεριφορά ενός ανοικτού συστήματος, που κάτω από ορισμένες συνθήκες, είναι ευαίσθητη στις αρχικές συνθήκες (συνθήκες εκκίνησης).
Δυναμικό σύστημα
Στον φυσικό κόσμο είναι κάθε εξελισσόμενη διαδικασία, ένα φυσικό φαινόμενο που εξελίσσεται στο χρόνο.
Χαρακτηριστική ιδιότητα
όλων των χαοτικών συστημάτων (και σίγουρα η πιο θεαματική) είναι η μεγάλη ευαισθησία τους στις αρχικές συνθήκες
Είναι γνωστή και ως το 'φαινόμενο της πεταλούδας' (μια ποιητική μεταφορά που πρώτος χρησιμοποίησε ο Edward Lorentz τη δεκαετία του 1960), σύμφωνα με την οποία, μια ανεπαίσθητη, φαινομενικά ασήμαντη μεταβολή, όπως το πέταγμα μιας πεταλούδας στον Αμαζόνιο, μπορεί να προκαλέσει (ή να αποτρέψει) βροχή στην Κίνα.
Σημαίνει ότι δυο απείρως γειτονικές τροχιές (με σχεδόν ταυτόσημες αρχικές συνθήκες), παραμένουν γειτονικές για μικρό μόνον χρονικό διάστημα και γρήγορα αρχίζουν να αποκλίνουν εκθετικά, κάτι που κάνει σύντομα το αρχικό μικρό σφάλμα (απόκλιση, αβεβαιότητα της μέτρησης) να μεγεθύνεται. Έτσι χάνεται γρήγορα η δυνατότητα πρόβλεψης της χρονικής τους εξέλιξης, της συμπεριφοράς τους.
σχόλιο: Η ευαισθησία-εξάρτηση από τις αρχικές συνθήκες, που φαίνεται σαν φαινομενική τυχαιότητα (ενώ στο σύστημα δεν υπεισέρχονται τυχαίες παράμετροι), δεν είναι ικανή από μόνη της να προκαλέσει χάος. Απαιτείται ταυτόχρονα να υπάρχει τοπολογική ανάμειξη (ή μεταβατικότητα).
Χαρακτηριστική ιδιότητα
όλων των χαοτικών συστημάτων (και σίγουρα η πιο θεαματική) είναι η μεγάλη ευαισθησία τους στις αρχικές συνθήκες
Είναι γνωστή και ως το 'φαινόμενο της πεταλούδας' (μια ποιητική μεταφορά που πρώτος χρησιμοποίησε ο Edward Lorentz τη δεκαετία του 1960), σύμφωνα με την οποία, μια ανεπαίσθητη, φαινομενικά ασήμαντη μεταβολή, όπως το πέταγμα μιας πεταλούδας στον Αμαζόνιο, μπορεί να προκαλέσει (ή να αποτρέψει) βροχή στην Κίνα.
Σημαίνει ότι δυο απείρως γειτονικές τροχιές (με σχεδόν ταυτόσημες αρχικές συνθήκες), παραμένουν γειτονικές για μικρό μόνον χρονικό διάστημα και γρήγορα αρχίζουν να αποκλίνουν εκθετικά, κάτι που κάνει σύντομα το αρχικό μικρό σφάλμα (απόκλιση, αβεβαιότητα της μέτρησης) να μεγεθύνεται. Έτσι χάνεται γρήγορα η δυνατότητα πρόβλεψης της χρονικής τους εξέλιξης, της συμπεριφοράς τους.
σχόλιο: Η ευαισθησία-εξάρτηση από τις αρχικές συνθήκες, που φαίνεται σαν φαινομενική τυχαιότητα (ενώ στο σύστημα δεν υπεισέρχονται τυχαίες παράμετροι), δεν είναι ικανή από μόνη της να προκαλέσει χάος. Απαιτείται ταυτόχρονα να υπάρχει τοπολογική ανάμειξη (ή μεταβατικότητα).
Πολυπλοκότητα
(complexity) Αν θέλαμε να συμπυκνώσουμε τα κύρια χαρακτηριστικά της θα λέγαμε ότι η πολυπλοκότητα σημαίνει τρία κυρίως πράγματα: μη γραμμικότητα, μη αναγωγικότητα και στοχαστικότητα.
(complexity) Αν θέλαμε να συμπυκνώσουμε τα κύρια χαρακτηριστικά της θα λέγαμε ότι η πολυπλοκότητα σημαίνει τρία κυρίως πράγματα: μη γραμμικότητα, μη αναγωγικότητα και στοχαστικότητα.
Γραμμικότητα
γραμμική είναι κάθε εξίσωση n μεταβλητών (αγνώστων) xi (1 ≤ i ≤ n), της μορφής:
a1x1 + a2 x2 + … + anxn = b
Λύση της είναι η ακολουθία των n τιμών si των xi , που την καθιστούν ταυτότητα.
Οι μεταβλητές σε μια γραμμική εξίσωση εμφανίζονται μόνον στην 1η δύναμη και δεν μπορούν να είναι ορίσματα τριγωνομετρικών, λογαριθμικών ή εκθετικών συναρτήσεων. Δεν μπορεί να περιλαμβάνουν επίσης γινόμενα ή ρίζες των μεταβλητών τους.
Στα γραμμικά συστήματα, που χαρακτηρίζονται από κανονική και ομαλή συμπεριφορά, ισχύει ότι το άθροισμα δυο λύσεων είναι κι αυτό λύση. Η ιδιότητά τους αυτή, που δεν ισχύει στα μη γραμμικά συστήματα, απλουστεύει πολύ τη λύση τους.
Μη γραμμικότητα
Η μη γραμμικότητα, που σημαίνει σχέση πιο πολύπλοκη από την απλή αναλογία, είναι το κυρίαρχο στοιχείο της φύσης σε όλα τα επίπεδα της φυσικής πραγματικότητας με κύριες συνέπειες το χάος και την αυτοοργάνωση. Μη γραμμικές είναι οι εξισώσεις που περιλαμβάνουν και όρους με τη μεταβλητή σε δυνάμεις μεγαλύτερες του 1, το γινόμενο xψ ή παραγώγους της μεταβλητής. Η αλληλεξάρτηση τους είναι που δημιουργεί την πολυπλοκότητα. Η αναλυτική επίλυσή τους είναι από πολύ δύσκολη έως αδύνατη, εκτός από ελάχιστες εξαιρετικές περιπτώσεις. Συνήθως προχωράμε σε απλούστευση, σε γραμμικοποίησή τους, αγνοώντας όρους που θεωρούμε αμελητέους.
a1x1 + a2 x2 + … + anxn = b
με a1 , a2 , … , an , b σταθερές, εF
(όπου F το σώμα των πραγματικών ή μιγαδικών αριθμών)
Λύση της είναι η ακολουθία των n τιμών si των xi , που την καθιστούν ταυτότητα.
Οι μεταβλητές σε μια γραμμική εξίσωση εμφανίζονται μόνον στην 1η δύναμη και δεν μπορούν να είναι ορίσματα τριγωνομετρικών, λογαριθμικών ή εκθετικών συναρτήσεων. Δεν μπορεί να περιλαμβάνουν επίσης γινόμενα ή ρίζες των μεταβλητών τους.
Στα γραμμικά συστήματα, που χαρακτηρίζονται από κανονική και ομαλή συμπεριφορά, ισχύει ότι το άθροισμα δυο λύσεων είναι κι αυτό λύση. Η ιδιότητά τους αυτή, που δεν ισχύει στα μη γραμμικά συστήματα, απλουστεύει πολύ τη λύση τους.
Μη γραμμικότητα
Η μη γραμμικότητα, που σημαίνει σχέση πιο πολύπλοκη από την απλή αναλογία, είναι το κυρίαρχο στοιχείο της φύσης σε όλα τα επίπεδα της φυσικής πραγματικότητας με κύριες συνέπειες το χάος και την αυτοοργάνωση. Μη γραμμικές είναι οι εξισώσεις που περιλαμβάνουν και όρους με τη μεταβλητή σε δυνάμεις μεγαλύτερες του 1, το γινόμενο xψ ή παραγώγους της μεταβλητής. Η αλληλεξάρτηση τους είναι που δημιουργεί την πολυπλοκότητα. Η αναλυτική επίλυσή τους είναι από πολύ δύσκολη έως αδύνατη, εκτός από ελάχιστες εξαιρετικές περιπτώσεις. Συνήθως προχωράμε σε απλούστευση, σε γραμμικοποίησή τους, αγνοώντας όρους που θεωρούμε αμελητέους.
Στοχαστικότητα
Aν η έκβαση ενός φαινομένου σε εξέλιξη, μπορεί να οδηγήσει σε δύο ή περισσότερα διαφορετικά αποτελέσματα (πχ, ζαριά, φύλο παιδιού που γεννιέται κλπ), άρα είναι αβέβαιη (ενδεχόμενη), ονομάζεται στοχαστικό φαινόμενο. Η άτακτη κίνηση (Brown) των μορίων ενός ρευστού είναι μια στοχαστική διαδικασία.
Η μελέτη τους, λόγω της μεταβλητότητας των δεδομένων, απαιτεί άλλη μαθηματική μεθοδολογία (Στατιστική, Πιθανότητες), που περιλαμβάνει τη διαφορετικότητα (αρχικών συνθηκών, συνθηκών πειράματος κλπ) και μπορεί να την εκφράσει.
έστω ότι θέλω να κάνω μια πρόβλεψη ή να πάρω μια απόφαση, σε ένα φαινόμενο, όπου γνωρίζω πως πέρα από νόμους και κανονικότητες, υπεισέρχονται συχνά αστάθμητοι παράγοντες, που αλλοιώνουν την έκβαση του φαινομένου.
πχ θέλω να κάνω πρόγνωση καιρού, να κάνω μια επένδυση στο χρηματιστήριο, να παίξω με ένα σύστημα στη ρουλέτα, να κάνω μια επιχειρηματική δραστηριότητα.
Μια κλασική προσέγγιση είναι: δεν το ακουμπάω με τη λογική, αναγνωρίζω ότι η έκβαση είναι απολύτως τυχαία και αβέβαιη, άρα μη προβλέψιμη, δηλαδή δεν παίζω στη ρουλέτα ή πάω ξέροντας ότι δεν μπορώ να κάνω τίποτα. Αναγνωρίζω ότι με το Θεό συμφωνίες δεν γίνονται, άρα παραιτούμαι από την απαίτηση της πρόβλεψης κι ότι κάτσει.
Τα οικονομικά φαινόμενα είναι στοχαστικά, δηλαδή υπεισέρχονται και τυχαίοι παράγοντες στην εξέλιξη τους, άρα μελετώνται καλύτερα, αν εισάγουμε εκτός από τις εξωγενείς μεταβλητές (που οι τιμές τους είναι δεδομένες) και μιας τυχαίας μεταβλητής στις εξισώσεις συμπεριφοράς, που ονομάζεται διαταρακτικός όρος και φέρνει καλύτερα αποτελέσματα και και κάθε στιγμή παίρνει τιμές με τυχαίο τρόπο μέσα από ένα σύνολο δυνατών τιμών. (πχ ρίψη ζαριού ή random walk-τυχαίος περίπατος)
Η στοχαστικότητα των πολύπλοκων φυσικών συστημάτων όπως και στα κβαντικά συστήματα είναι ευγενές δυναμικό στοιχείο και όχι υποκειμενική αδυναμία παρατήρησης. Αυτό είναι και η πεμπτουσία της χαοτικής δυναμικής.
Η μελέτη τους, λόγω της μεταβλητότητας των δεδομένων, απαιτεί άλλη μαθηματική μεθοδολογία (Στατιστική, Πιθανότητες), που περιλαμβάνει τη διαφορετικότητα (αρχικών συνθηκών, συνθηκών πειράματος κλπ) και μπορεί να την εκφράσει.
έστω ότι θέλω να κάνω μια πρόβλεψη ή να πάρω μια απόφαση, σε ένα φαινόμενο, όπου γνωρίζω πως πέρα από νόμους και κανονικότητες, υπεισέρχονται συχνά αστάθμητοι παράγοντες, που αλλοιώνουν την έκβαση του φαινομένου.
πχ θέλω να κάνω πρόγνωση καιρού, να κάνω μια επένδυση στο χρηματιστήριο, να παίξω με ένα σύστημα στη ρουλέτα, να κάνω μια επιχειρηματική δραστηριότητα.
Μια κλασική προσέγγιση είναι: δεν το ακουμπάω με τη λογική, αναγνωρίζω ότι η έκβαση είναι απολύτως τυχαία και αβέβαιη, άρα μη προβλέψιμη, δηλαδή δεν παίζω στη ρουλέτα ή πάω ξέροντας ότι δεν μπορώ να κάνω τίποτα. Αναγνωρίζω ότι με το Θεό συμφωνίες δεν γίνονται, άρα παραιτούμαι από την απαίτηση της πρόβλεψης κι ότι κάτσει.
Πρόκειται για μια φιλοσοφική στάση ζωής, που ικανοποιούσε
όλα (και συνεχίζει να ικανοποιεί και σήμερα κάποια) άτομα της
προεπιστημονικής περιόδου της ανθρωπότητας, που αναγνωρίζουν και
σέβονται την αβεβαιότητα και το ρόλο του τυχαίου και ζουν μια χαρά με
αυτό.
Τα οικονομικά φαινόμενα είναι στοχαστικά, δηλαδή υπεισέρχονται και τυχαίοι παράγοντες στην εξέλιξη τους, άρα μελετώνται καλύτερα, αν εισάγουμε εκτός από τις εξωγενείς μεταβλητές (που οι τιμές τους είναι δεδομένες) και μιας τυχαίας μεταβλητής στις εξισώσεις συμπεριφοράς, που ονομάζεται διαταρακτικός όρος και φέρνει καλύτερα αποτελέσματα και και κάθε στιγμή παίρνει τιμές με τυχαίο τρόπο μέσα από ένα σύνολο δυνατών τιμών. (πχ ρίψη ζαριού ή random walk-τυχαίος περίπατος)
Η στοχαστικότητα των πολύπλοκων φυσικών συστημάτων όπως και στα κβαντικά συστήματα είναι ευγενές δυναμικό στοιχείο και όχι υποκειμενική αδυναμία παρατήρησης. Αυτό είναι και η πεμπτουσία της χαοτικής δυναμικής.
Η στοχαστικότητα γίνεται εν γένει ιδιότητα των μη γραμμικών συστημάτων, λόγω της δύναμης αστάθειας (ευαισθησία ως προς τις αρχικές συνθήκες) και αποτελεί τη γέφυρα μεταξύ συντηρητικών και μη συντηρητικών (καταναλισκόντων) συστημάτων. Τα στοχαστικά δυναμικά συστήματα, με την έννοια των Μαρκοβιανών διαδικασιών, αποτελούν το νέο «ζωολογικό κήπο» της επιστήμης, αφού σε αυτά περιέχονται όλα τα μοντέλα που χρειάζεται κανείς για να περιγράψει την φυσική πραγματικότητα στην πολυπλοκότητά της, είτε πρόκειται για δημιουργία νέων μορφών (patterns), είτε για φράκταλ φυσικές δομές, είτε για τη δύναμη των πληθυσμών, είτε πρόκειται για πολύπλοκες λειτουργίες σε επίπεδο οικολογίας, οικονομίας, τεχνητής νοημοσύνης κλπ.
Αυτοοργάνωση
(self-organization) στα χαοτικά συστήματα, όπως άλλωστε και στα κβαντικά, εμφανίζεται ένα ακατανόητο, με τις κλασικές αντιλήψεις, φαινόμενο. Διαδικασίες που συμβαίνουν σε διαφορετικά και πολύ απομακρυσμένα σημεία του χώρου (που η μεταξύ τους αλληλεπίδραση είναι μηδενική, αφού η εμβέλεια της είναι τοπικά περιορισμένη), συσχετίζονται, σαν να αντιλαμβάνεται το ένα τις μεταβολές του άλλου, συντονίζονται.
Ένα εντυπωσιακό παράδειγμα είναι το φαινόμενο της παράσυρσης (entrainment) (ή της 'λογικής του σμήνους', με ελαστικά, αξιόπιστα, ευφυή συστήματα, χαμηλών υπολογιστικών απαιτήσεων, που αξιοποιούν τοπικού χαρακτήρα πληροφορία, πετυχαίνοντας τελικά αποτέλεσμα χωρίς κεντρικό-σφαιρικό σχέδιο), ο απόλυτος συντονισμός βιολογικών ταλαντωτών, όπως ένα πλήθος χιλιάδων αρσενικών πυγολαμπίδων την περίοδο της αναπαραγωγής τους στη ΝΑ Ασία (επηρεάζοντας η μια την άλλη, χωρίς την εποπτεία, την παρέμβαση κάποιου κεντρικού συντονιστή ή 'ηγέτη').
Ένα απλό παράδειγμα αυτοοργάνωσης, που χρησιμοποιούσε συχνά σε συνεντεύξεις του ο Πριγκοζίν, έχουμε στη θερμική διάχυση: έστω ότι σε ένα δοχείο έχουμε ένα ομογενές μείγμα «γαλάζιων» και «ερυθρών» μορίων, δύο διαφορετικών αερίων που δεν αντιδρούν μεταξύ τους χημικά. Αν το θερμάνουμε από τη μια μόνο πλευρά, τα «γαλάζια» μόρια συσσωρεύονται στη μία πλευρά ενώ τα «ερυθρά» μόρια στην άλλη. Σχηματίζεται δηλαδή μια οργάνωση, που δεν μπορεί να προκύψει σε συνθήκες ισορροπίας.
Τρισεκατομμύρια μόρια δηλαδή αρχίζουν ξαφνικά να περιστρέφονται ομοιόμορφα, με την ίδια συχνότητα, σαν να έχουν συντονιστεί από έναν αόρατο μαέστρο.
Αυτοί οι στρόβιλοι αποτελούν σχήματα οργάνωσης γνωστά
ως κυψέλες του Benard, όπου δισεκατομμύρια μόρια συσχετίζονται, ώστε να
μορφοδομηθούν οι στρόβιλοι. Συνεπώς μακριά από την ισορροπία δημιουργείται τάξη.
φράκταλ
πρόκειται για γεωμετρικά σχήματα με 'απείρως περίπλοκη μορφή', για 'μαγικές εικόνες', σαν τη διπλανή, που προκύπτουν από την επαναληπτική διαδικασία (αριθμητική ή λογική) μιας απλής εντολής (αλγόριθμου).ο όρος fractal προτάθηκε το 1975 από τον Μάντελμπροτ (Benoit Mandelbrot) και προέρχεται από το λατινικό fractus, που σημαίνει σπασμένος, κλασματικός.
ένα σημαντικό χαρακτηριστικό τους είναι πως το μήκος της περιμέτρου τους αλλάζει θεαματικά, αλλάζοντας μονάδα μέτρησης και γίνεται άπειρο για απειροστή μονάδα μέτρησης, ενώ το εμβαδόν τους είναι βέβαια πεπερασμένο.
αυτοομοιότητα
κλασματικές διαστάσεις
ή διάσταση ομοιότητας ή γεωμετρικό μέτρο του Hausdorff.
Μια απλή ευκλείδεια γραμμή μπορεί να μην έχει πάχος, άρα να είναι τοπολογικά μονοδιάστατη (συνεχής μεν καμπύλη, αλλά πουθενά διαφορίσιμη, θα έλεγαν οι φίλοι μας οι μαθηματικοί). Αν όμως πάρουμε μια λίγο πιο τζουρτζουλωτή, σαν αυτή την πασίγνωστη που έφτιαξε το 1904 ο Σουηδός μαθηματικός Helgs von Koch στην παρακάτω εικόνα, αυτή 'γεμίζει' μέχρι ένα σημείο τον δισδιάστατο χώρο, άρα η διάσταση της μπορεί να έχει ενδιάμεση τιμή, μεταξύ του 1 και του 2, πχ 1,268.
Το εντυπωσιακό εδώ είναι ότι ενώ το εμβαδόν του τελικού σχήματος, μετά από ν βήματα (στο ν-οστό επίπεδο διαίρεσης) είναι πεπερασμένο, υπολογίζεται πως είναι τα 8/5 του εμβαδού του αρχικού ισόπλευρου τριγώνου, το μήκος της περιμέτρου του γίνεται άπειρο.
Ξεκινώντας τώρα από ένα τρίγωνο, αντί για ευθύγραμμο τμήμα και εφαρμόζοντας τον ίδιο αλγόριθμο, μπορούμε (με την ίδια ακριβώς λογική) να φτιάξουμε κάτι που θυμίζει νιφάδα χιονιού, εξ ου και η ονομασία του Koch snowflake, που βλέπουμε εδώ.
Η σκόνη του Cantor
Το σύνολο του Cantor (ή 'σκόνη του Κάντορ΄) και ο ατσάλινος Πύργος του Eiffel, κατασκευής του 1889, μια ευφυής εφαρμογή του τριγώνου του Sierpinski σε κανονικό τετράεδρο, με τετράγωνη βάση πλευράς 100 μ, ύψος 300 μ και βάρος μόνον 8.000 τόνους.
Ένα από τα πιο γνωστά fractals είναι και το τρίγωνο (ή πλέγμα) του Sierprinski:
εδώ η διαδικασία δημιουργίας του και η απεικόνιση του σε 3 διαστάσεις. Η κλασματική του διάσταση είναι περίπου 1,585 (και προκύπτει ως log2/log3), όπου Ν(ε) ο αριθμός των αυτοόμοιων δομών του γραμμικού μεγέθους ε, που χρειάζεται για να καλύψει όλη τη δομή Γ.
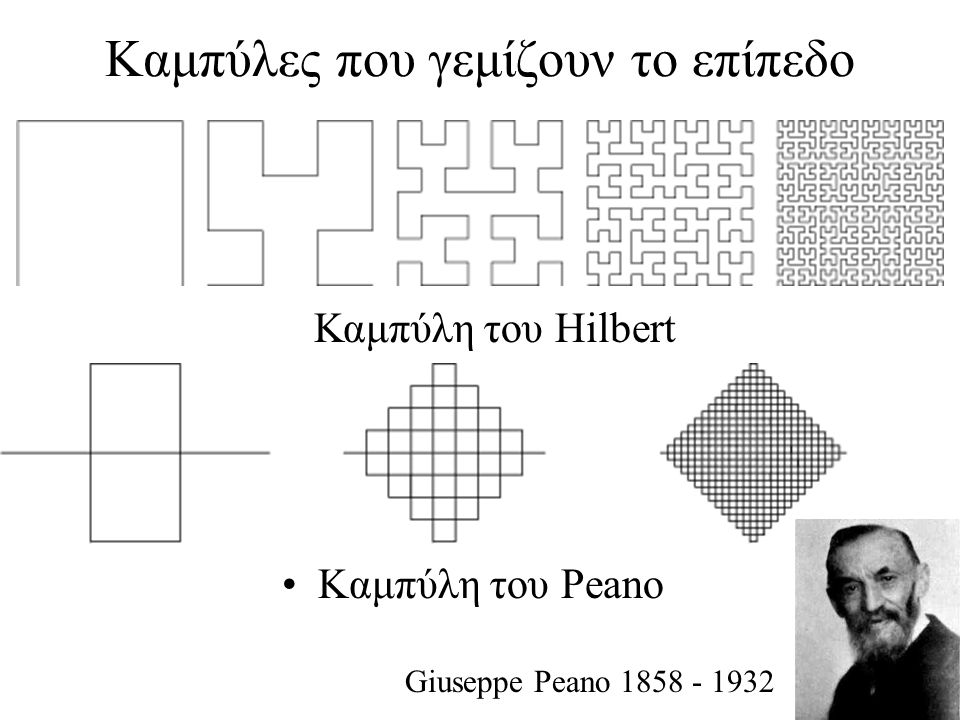
καμπύλη του Peano
The first type begins with an S-shape, which winds from the southwest corner of its bounding square to end up in the northeast corner:
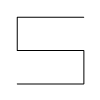
Copies are arranged in a 3×3 grid, with every other copy being rotated 90 degrees:
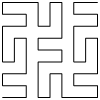
And finally the copies are joined in a sort of N-shaped route (up the left column, down the middle column, up the right column): Repeating the process gives the first type of Wund
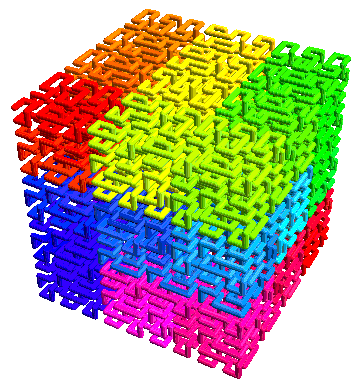
είναι ένας δεκαδικός αριθμός (πχ 1,834 για τη καμπύλη Holbert 4ης τάξης) μεταξύ δυο ακεραίων (πχ του 1 και του 2), που δείχνει πόσο καλά γεμίζει μια μονοδιάστατη γραμμή μια επίπεδη δισδιάστατη επιφάνεια.
μορφοκλασματική γεωμετρία
"τα σύννεφα δεν είναι σφαίρες, τα βουνά δεν είναι κώνοι, οι ακτές δεν είναι κύκλοι και ο φλοιός του δέντρου δεν είναι ομαλός, ούτε η αστραπή ταξιδεύει σε ευθεία γραμμή " Benoit Mandelbrot.
τυχαιότητα
από τα μαθηματικά της φράκταλ γεωμετρίας προκύπτουν τρεις καταστάσεις τυχαιότητας: η 'ήπια', η 'αργή' και η 'ατίθαση'.
Μη αναγωγικότητα
Η αδυναμία αναγωγής του συνόλου στα μέρη του. Αφορά τα κβαντικά και τα πολύπλοκα συστήματα, όπου το όλον καθορίζει το μέρος, αλλά δεν εξηγείται από αυτό, δεν μπορεί να θεωρηθεί σαν απλό άθροισμα των μερών του. Σε κάθε ιεραρχικό επίπεδο έχουμε ενδογενείς νόμους, που οφείλονται μεν στους νόμους του υποκειμένου επιπέδου, αλλά δεν ανάγονται σε αυτούς.
Η αλλαγή κλίμακας δεν δίνει αναγώγιμες έννοιες. Η θερμοκρασία και η πίεση (μέση τιμή της ορμής) ενόςαερίου είναι συλλογικές ιδιότητες-έννοιες του φαινομενολογικού επιπέδου, που δεν υφίστανται στο μικροσκοπικό επίπεδο. Ένα ηλεκτρόνιο πχ δεν έχει θερμοκρασία (μέση τιμή της ενέργειας), μόνον κίνηση.
Στη
θεωρία της πολυπλοκότητας ξεπερνιέται ο κλασσικός αναγωγισμός και
αναδεικνύεται η ευρηματικότητα της φύσης να χρησιμοποιεί, σε κάθε
περιοχή φυσικών φαινομένων, τον αντίστοιχο «αλγόριθμο» και την
«κατάλληλη δυναμική», χωρίς να είναι δυνατόν οι δυναμικές υψηλότερου επιπέδου να αναχθούν σε κάποιες ή κάποια θεμελιώδη δυναμική χαμηλότερου επιπέδου.
Η αδυναμία αναγωγής του συνόλου στα μέρη του. Αφορά τα κβαντικά και τα πολύπλοκα συστήματα, όπου το όλον καθορίζει το μέρος, αλλά δεν εξηγείται από αυτό, δεν μπορεί να θεωρηθεί σαν απλό άθροισμα των μερών του. Σε κάθε ιεραρχικό επίπεδο έχουμε ενδογενείς νόμους, που οφείλονται μεν στους νόμους του υποκειμένου επιπέδου, αλλά δεν ανάγονται σε αυτούς.
Η αλλαγή κλίμακας δεν δίνει αναγώγιμες έννοιες. Η θερμοκρασία και η πίεση (μέση τιμή της ορμής) ενόςαερίου είναι συλλογικές ιδιότητες-έννοιες του φαινομενολογικού επιπέδου, που δεν υφίστανται στο μικροσκοπικό επίπεδο. Ένα ηλεκτρόνιο πχ δεν έχει θερμοκρασία (μέση τιμή της ενέργειας), μόνον κίνηση.
Στη
θεωρία της πολυπλοκότητας ξεπερνιέται ο κλασσικός αναγωγισμός και
αναδεικνύεται η ευρηματικότητα της φύσης να χρησιμοποιεί, σε κάθε
περιοχή φυσικών φαινομένων, τον αντίστοιχο «αλγόριθμο» και την
«κατάλληλη δυναμική», χωρίς να είναι δυνατόν οι δυναμικές υψηλότερου επιπέδου να αναχθούν σε κάποιες ή κάποια θεμελιώδη δυναμική χαμηλότερου επιπέδου. Διαστάσεις
ενός δυναμικού συστήματος είναι ο ελάχιστος αριθμός (το πλήθος) των δυναμικών μεταβλητών που απαιτούνται για να το περιγράψουν.
Τροχιά
ή καμπύλη στο χώρο των φάσεων (των καταστάσεων) είναι η η-διάστατη παράσταση της λύσης, στον
χώρο των δυναμικών μεταβλητών (εκείνων που εξαρτώνται από τον χρόνο).
αν πχ θεωρήσω έναν δυσδιάτατο χώρο θέσης-ταχύτητας, έχω ένα σημείο για κάθε κατάσταση και μια γραμμή για τη χρονική εξέλιξη του συστήματος.
αν πχ θεωρήσω έναν δυσδιάτατο χώρο θέσης-ταχύτητας, έχω ένα σημείο για κάθε κατάσταση και μια γραμμή για τη χρονική εξέλιξη του συστήματος.
Διακλαδώσεις
Μεταβολές στις παραμέτρους που επιφέρουν ποιοτική μεταβολή στη δομή των λύσεων
Σημεία διακλάδωσης
Ονομάζονται οι τιμές των παραμέτρων..
Διαφορισιμότητα
Είναι η δυνατότητα περιγραφής της μεταβολής με διαφορίσιμες συναρτήσεις.
Τα
δυναμικά συστήματα περιγράφονται μαθηματικά από (διαφορικές) εξισώσεις
(μιας ή περισσότερων μεταβλητών), που μια τουλάχιστον μεταβλητή τους,
εξαρτάται από τον χρόνο.
Γραμμικότητα
Σχετίζεται
με τη συνέχεια, τις ομαλές μεταβολές, τη δυνατότητα αναγωγής καμπυλών (τοπικά) σε μικρά ευθύγραμμα τμήματα, άρα παραγωγίσιμων σε κάθε τους
σημείο.
Μη γραμμικότητα
Ενώ οι μη γραμμικές διαφορικές εξισώσεις, γενικά δεν επιλύονται, με την πάροδο του χρόνου εμφανίζουν ευστάθεια, συγκλίνουν δηλαδή τελικά σε ένα σημείο (όπως πχ μια έλικα).
Ευστάθεια
Μια
λύση (για κάποια χρονική στιγμή) χαρακτηρίζεται ευσταθής αν ισχύει ότι:
αν άλλες λύσεις βρίσκονται κοντά της σε ορισμένο χρόνο, τότε θα
βρίσκονται κοντά της, και για επόμενους χρόνους, δηλαδή την πλησιάζουν
ασυμπτωτικά, συγκλίνουν.
Μακράν της θερμοδυναμικής ισορροπίας
(far from equilibrium thermodynamics)
μια χημική αντίδραση κοντά στο τέλος της, που εξελίσσεται με μικρή ταχύτητα, έχει άλλα χαρακτηριστικά από μια άλλη που η ταχύτητά της είναι μεγάλη.
(far from equilibrium thermodynamics)
μια χημική αντίδραση κοντά στο τέλος της, που εξελίσσεται με μικρή ταχύτητα, έχει άλλα χαρακτηριστικά από μια άλλη που η ταχύτητά της είναι μεγάλη.
Μη διατηρητικά
(ή ανοικτά) συστήματα είναι εκείνα που ανταλλάσσουν μάζα και ενέργεια με το περιβάλλον (τέτοια είναι τα περισσότερα φυσικοχημικά συστήματα).
(ή ανοικτά) συστήματα είναι εκείνα που ανταλλάσσουν μάζα και ενέργεια με το περιβάλλον (τέτοια είναι τα περισσότερα φυσικοχημικά συστήματα).
Μη γραμμικά
αυτά που αποκλίνουν από τη σχέση απλής αναλογίας δυο μεγεθών, ασυνεχή
αυτά που αποκλίνουν από τη σχέση απλής αναλογίας δυο μεγεθών, ασυνεχή
Τελεστής
Έννοια που εισήχθη αρχικά στα πλαίσια της κβαντικής θεωρίας και επεκτάθηκε αργότερα σε άλλους πεδία της Φυσικής, κυρίως στην στατιστική μηχανική.
Πρόκειται
για μια συνταγή, μια εντολή, που καθορίζει τον τρόπο δράσης πάνω σε μια
συνάρτηση, της επιβάλλει μια μαθηματική πράξη (πχ την πολλαπλασιάζει ή
την ολοκληρώνει ή την διαφορίζει κλπ), με αποτέλεσμα να την
μετασχηματίζει εν γένει σε μια νέα διαφορετική συνάρτηση.
Χώρος των φάσεων
(phase space) είναι ένα διάγραμμα σε ένα νοητό χώρο θέσης-ορμής ή θέσης-ταχύτητας (x-p ή x-u, για κάθε βαθμό ελευθερίας του συστήματος), που εμπεριέχει πολύ περισσότερες πληροφορίας για την εξέλιξη του συστήματος, από τον γνωστό μας χωρόχρονο, τον θεσιογραφικό χώρο (x-t).
Ένα σημείο στο χώρο των φάσεων παριστάνει την κατάσταση του συστήματος για μια συγκεκριμένη χρονική στιγμή. Όσο ο χρόνος (που εδώ υπεισέρχεται σιωπηρά, μέσω της ταχύτητας = ρυθμός μεταβολής της μετατόπισης) μεταβάλλεται, το σημείο μετακινείται, διαγράφοντας μια τροχιά.
Ελκυστής
(attractor)
Ανάλογα με την αρχική συνθήκη, οι τροχιές έλκονται από ένα σημείο ή σύνολο σημείων ή διαφεύγουν στο άπειρο. Το σύνολο των σημείων που έλκει έναν αριθμό τροχιών ονομάζεται ελκυστής. Ένα απλό παράδειγμα, μια ακίνητη πέτρα στη ροή του νερού ενός ποταμού, πίσω από την οποία δημιουργείται μια δίνη.
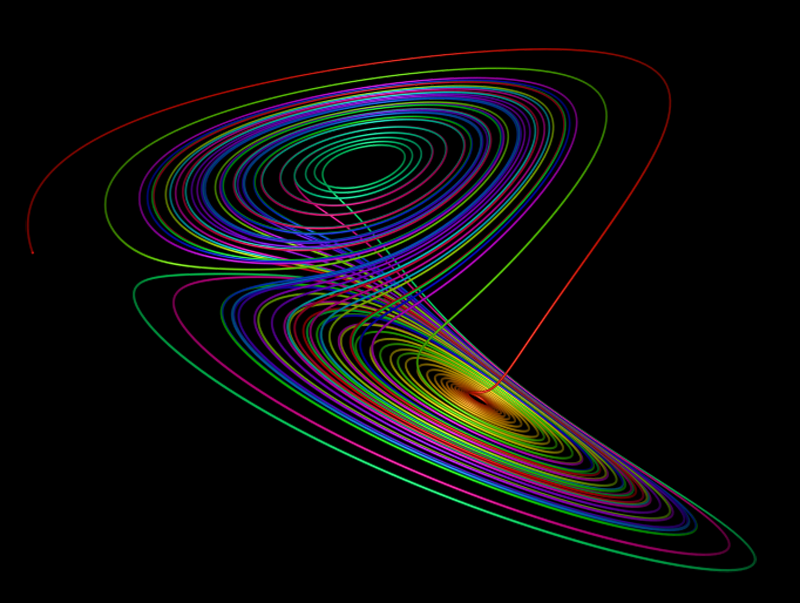
Δεξιά ο ελκυστής του Lorentz. Η τροχιά (που κάθε σημείο της εκφράζει την κατάσταση του συστήματος σε μια χρονική στιγμή) εμφανίζει άπειρη πολυπλοκότητα. Ενώ κινείται παγιδευμένη μέσα σε μια περιορισμένη, ΄φραγμένη΄ περιοχή του χώρου, συνεχίζει να κινείται επ άπειρον, χωρίς να τερματίζει ποτέ!
Δημιουργεί διαρκώς καινούργιους βρόγχους, που δεν τέμνονται ποτέ, δεν επαναλαμβάνεται δηλαδή ποτέ (δεν γίνεται περιοδική) !!! Πρόκειται για καθαρή αταξία, που ταυτόχρονα όμως αποτελεί ένα νέο είδος τάξης.
Η εικόνα παριστάνει ένα μέρος της τροχιάς της λύσης (για ορισμένο χρονικό διάστημα, αφού ο ελκυστής δεν είναι δυνατόν να σχεδιαστεί ολόκληρος), ενός συστήματος από τρεις διαφορικές εξισώσεις:
dx/d t= a(y-x)
Ο ανθρώπινος χαρακτήρας δεν είναι παρά ένας χαοτικός ελκυστής που, με τα αόρατα φράγματα που βάζει ανάμεσα σε αυτόν και τον υπόλοιπο κόσμο, καθορίζει μια προσωπικότητα, κάνοντας χρήση περιορισμένου αριθμού καταστάσεων και αποκλείοντας όλες τις άλλες δυνατές καταστάσεις. Έτσι βέβαια πετυχαίνει να έχει ένα εγώ, αλλιώς δεν θα υπήρχε, δεν θα ήταν 'αυτός'.
Χώρος των φάσεων
(phase space) είναι ένα διάγραμμα σε ένα νοητό χώρο θέσης-ορμής ή θέσης-ταχύτητας (x-p ή x-u, για κάθε βαθμό ελευθερίας του συστήματος), που εμπεριέχει πολύ περισσότερες πληροφορίας για την εξέλιξη του συστήματος, από τον γνωστό μας χωρόχρονο, τον θεσιογραφικό χώρο (x-t).
Ένα σημείο στο χώρο των φάσεων παριστάνει την κατάσταση του συστήματος για μια συγκεκριμένη χρονική στιγμή. Όσο ο χρόνος (που εδώ υπεισέρχεται σιωπηρά, μέσω της ταχύτητας = ρυθμός μεταβολής της μετατόπισης) μεταβάλλεται, το σημείο μετακινείται, διαγράφοντας μια τροχιά.
Ελκυστής
(attractor)
Ανάλογα με την αρχική συνθήκη, οι τροχιές έλκονται από ένα σημείο ή σύνολο σημείων ή διαφεύγουν στο άπειρο. Το σύνολο των σημείων που έλκει έναν αριθμό τροχιών ονομάζεται ελκυστής. Ένα απλό παράδειγμα, μια ακίνητη πέτρα στη ροή του νερού ενός ποταμού, πίσω από την οποία δημιουργείται μια δίνη.Δεξιά ο ελκυστής του Lorentz. Η τροχιά (που κάθε σημείο της εκφράζει την κατάσταση του συστήματος σε μια χρονική στιγμή) εμφανίζει άπειρη πολυπλοκότητα. Ενώ κινείται παγιδευμένη μέσα σε μια περιορισμένη, ΄φραγμένη΄ περιοχή του χώρου, συνεχίζει να κινείται επ άπειρον, χωρίς να τερματίζει ποτέ!
Δημιουργεί διαρκώς καινούργιους βρόγχους, που δεν τέμνονται ποτέ, δεν επαναλαμβάνεται δηλαδή ποτέ (δεν γίνεται περιοδική) !!! Πρόκειται για καθαρή αταξία, που ταυτόχρονα όμως αποτελεί ένα νέο είδος τάξης.
Η εικόνα παριστάνει ένα μέρος της τροχιάς της λύσης (για ορισμένο χρονικό διάστημα, αφού ο ελκυστής δεν είναι δυνατόν να σχεδιαστεί ολόκληρος), ενός συστήματος από τρεις διαφορικές εξισώσεις:
dx/d t= a(y-x)
dy/dt = x(b-)z-y
dz/dt = xy-cz
που περιέχουν δύο μη γραμμικούς όρους (τους xz και xy) και μοντελοποιούν ρεύματα μεταφοράς θερμότητας μέσα σε ένα ρευστό (εδώ για a=10, b=28, c=8/3).
Ο ανθρώπινος χαρακτήρας δεν είναι παρά ένας χαοτικός ελκυστής που, με τα αόρατα φράγματα που βάζει ανάμεσα σε αυτόν και τον υπόλοιπο κόσμο, καθορίζει μια προσωπικότητα, κάνοντας χρήση περιορισμένου αριθμού καταστάσεων και αποκλείοντας όλες τις άλλες δυνατές καταστάσεις. Έτσι βέβαια πετυχαίνει να έχει ένα εγώ, αλλιώς δεν θα υπήρχε, δεν θα ήταν 'αυτός'.
Ιδιοσυναρτήσεις
του συγκεκριμένου τελεστή, όπου η νέα συνάρτηση είναι η ίδια (πχ η συνάρτηση eκx παραμένει αναλλοίωτη στην παραγώγιση, αφού προκύπτει η κ.eκx), απλά πολλαπλασιασμένη με μια σταθερά, έναν παράγοντα κ που ονομάζεται ιδιοτιμή.
Τελεστής Peron-Frobenius U
είναι ο τελεστής της εξέλιξης του χάους
Απεικόνιση του αρτοποιού
Είναι ένα καλό παράδειγμα ντετερμινιστικού χάους. Πρόκειται για ένα μετασχηματισμό (γενίκευση της απεικόνισης του Bernoulli), με δύο αντί μιας μεταβλητών, που διαστέλλει, διπλασιάζει (με θετικό εκθέτη Liapounov) τη μια διάσταση, συστέλλοντας την άλλη (με αρνητικό εκθέτη Liapounov).
Έτσι από ένα αρχικό τετράγωνο που συμπιέζεται πάμε σε ορθογώνιο
παραλληλόγραμμο και μετά κόβοντάς το στη μέση ανακατασκευάζει το
τετράγωνο, που τελικά διατηρείται.
Διαδοχικοί μετασχηματισμοί δημιουργούν όλο και περισσότερες στενότερες λωρίδες. Έτσι
δυο σημεία που αρχικά δεν ήταν δυνατόν να διακριθούν, καταλήγουν μετά από χρόνο να διακρίνονται, με την επίδραση της διαστελλόμενης
συντεταγμένης.
Το
παράδοξο πλεονέκτημα της είναι ότι αντιστρέφοντας τις μεταβλητές
(αλλάζοντας το ρόλο των συντεταγμένων), μπορεί να αντιστραφεί ως προς
τον χρόνο, είναι δηλαδή ανάδρομη, παραμένοντας ντετερμινιστική και
περιγράφει μια χαοτική δυναμική.
Η
αρχική επιτυχία της κλασικής και της κβαντικής φυσικής καθυστέρησε την
επέκτασή της στη μη ισορροπία, στα ασταθή δυναμικά συστήματα. Η περιγραφή με όρους τροχιών ισχύει μόνον αν είναι γνωστές με άπειρη ακρίβεια οι αρχικές συνθήκες.
Ντετερμινιστικά
ή αιτιοκρατικά είναι αυτά στα οποία δεν υπεισέρχονται τυχαίοι παράγοντες, άρα το παρελθόν και το μέλλον τους μπορεί να γίνουν γνωστά (και ορίζονται μονοσήμαντα), αν γνωρίζουμε το παρόν τους.
Μη ντετερμινιστικά
Είναι τα συστήματα στα οποία υπεισέρχονται τυχαίοι παράγοντες, εμφανίζουν σε μεγάλους μελλοντικούς χρόνους χαοτική απόκριση, δηλαδή απρόβλεπτη συμπεριφορά.
Σύμφωνα με την αντίληψη του ντετερμινισμού, οτιδήποτε συμβαίνει, είναι επακριβώς προσδιορισμένο από πριν, αφού για το καθετί υπάρχει μια αιτία. Τίποτα δεν δημιουργείται από μηδέν, το σύμπαν διέπεται από μια απόλυτη αναγκαιότητα, άρα πίσω από κάθε συμβάν-αποτέλεσμα υπάρχει πάντα ένα αίτιο που το προκάλεσε. Κάθε γεγονός το οποίο εμπεριέχει ανθρώπινη δράση συνδέεται με αιτιώδη αλυσιδωτή σχέση με τις προγενέστερες καταστάσεις. Δεν υπάρχουν ανεξήγητα η τυχαία γεγονότα. Αν γνωρίζουμε τις αρχικές συνθήκες, μπορούμε να προβλέψουμε το μέλλον και να ανασυνθέσουμε το παρελθόν.Πρόκειται για μια συμβατικά αντίληψη χρήσιμη και αξιόπιστη για τα ευσταθή συστήματα, αλλά και για τα ασταθή μέχρι τον ορίζοντα της προβλεψιμότητάς τους.
Το Χάος, όπως άλλωστε και η κβαντική φυσική, υπερβαίνει την αιτιοκρατία, σπάει τη συμμετρία ανάμεσα στο μέλλον και το παρελθόν και εισάγει έναν πιθανολογικό τρόπο σκέψης, που μοιάζει να είναι μια στενή μέση οδός ανάμεσα σε μια ανελεύθερη μηχανιστική αιτιοκρατία και την άσκοπη τυχαιότητα. Ανάμεσα σε έναν ελέγξιμο ντετερμινιστικό κόσμο με τυφλούς νόμους και αναπόφευκτα γεγονότα (έναν θεό που δεν αφήνει κανένα περιθώριο για ελευθερία, αλλά ούτε και ευθύνη) και σε έναν κόσμο έρμαιο της τύχης (έναν θεό που παίζει την τύχη μας στα ζάρια), υπάρχει η νέα δυνατότητα περιγραφής του κόσμου μας με πιθανότητες, με δυνατότητες, χωρίς όμως απόλυτες βεβαιότητες.
Η αβεβαιότητα συνυπάρχει με την καινοτομία, την ελευθερία και τη δημιουργικότητα.
.jpg)
0 σχόλια:
Δημοσίευση σχολίου