Ο Μικρός Κόσμος

Μια ενδιαφέρουσα νέα θεωρία

εισαγωγή

Ένας οποιοσδήποτε πληθυσμός μπορεί να θεωρηθεί σαν ένα κοινωνικό δίκτυο, που ξεκινώντας από ένα τυχαίο άτομο, μπορούμε να καταλήξουμε (μέσω μιας συντομότατης διαδρομής, μέσα από απί-στευτα λίγους ενδιάμεσους συνδέσμους-κόμβους), σε ένα άλλο άγνωστο άτομο, τυχαία επιλεγμένο, κοινωνικά και γεωγραφικά απομακρυσμένο.

Σαν δίκτυο μπορεί να θεωρηθεί μια ανθρώπινη κοινωνία, αλλά και το σύνολο των νευρώνων του εγκεφάλου ή οι σελίδες του internet. Η μαθηματική μελέτη της δομής των δικτύων (με εργαλεία από τη Θεωρία των Πιθανοτήτων και τη θεωρία των Γράφων), του αριθμού των συνδέσμων, του τρόπου σύνδεσή τους και των εγγενών ιδιοτήτων τους,  είναι σε εξέλιξη στις μέρες μας. 

Σημαντικό στοιχείο αποτελεί η δυσλειτουργία (έως και αποδιοργάνωση) που μπορεί να επιφέρει σε ένα δίκτυο η διαγραφή ενός και μόνον κόμβου.

Στον καθένα μας έχει τύχει (πάνω από μια φορά), συζητώντας με κάποιον άγνωστο που μόλις έχουμε γνωρίσει, να διαπιστώσουμε έκπληκτοι πως συμπτωματικά γνωρίζουμε κι οι δυο  ένα τρίτο πρόσω-πο, έχουμε κάποιον κοινό γνωστό.

Το κλείσιμο της κουβέντας είναι πάντα: 'για δες τι μικρός που είναι ο κόσμος!'

η νέα θεωρία

Από πειράματα που έκαναν, τη δεκαετία του 1960, ερευνητές στις ΗΠΑ και κύρια ο Ούγγρος Stanley Milgram, προκύπτει ότι με 6 μόλις βήματα (κατά μέσον όρο) μπορεί ένα μήνυμα να φτάσει από έναν τυχαίο πολίτη των ΗΠΑ,  σε έναν οποιονδήποτε άλλο.

Ο Μίλγκραμ δημοσίευσε τα αποτελέσματα του τον Μάιο του 1967, στην εργασία του: "The Small World Problem".

Οι εφαρμογές της νέας θεωρίας του 'μικρού κόσμου' αφορούν στη σχεδίαση ηλεκτρικών κυκλωμάτων ή των γραμμών του μετρό, την πλοήγηση με GPS, αλλά και την αναζήτηση στο internet, στα δίκτυα γενετικής αλληλεπίδρασης ή αλληλεπίδρασης πρω-τεϊνών κλπ
Μπορεί να φανεί χρήσιμη ακόμη και στην προστασία της ανθρωπότητας από ιούς και επιδημίες.

το θεώρημα των τεσσάρων χρωμάτων

Πόσα χρώματα (κατ΄ελάχιστον) απαιτούνται για τον χρωμα-τισμό ενός χάρτη, έτσι ώστε να μην υπάρχουν δύο γειτονικές περιοχές με τα ίδια χρώματα. 
Ένα πρόβλημα που τέθηκε ήδη από το 1852, από τον Άγγλο Frederick Gathrie, αλλά λύθηκε μόνον το 1976, από τους K. Appel και W. Haken. Ήταν το πρώτο σημαντικό θεώρημα που αποδείχθηκε με τη χρήση ΗΥ. 

Το θεώρημα ισχύει με την προϋπόθεση ότι κάθε χώρα θα πρέπει να είναι μία περιοχή, που απλά ενώνεται ή είναι γειτονική με μια άλλη, αλλιώς τα τέσσερα χρώματα μπορεί να μην είναι αρκετά. 

Παράδειγμα το απομονωμένο στη Βαλτική Καλίνιν-γκραντ. που ενώ αποτελεί μέρος της Ρωσίας, βρίσκεται γεωγραφικά μεταξύ Πολωνίας και  Λιθουανίας. 

Ο χρωματισμός ενός χάρτη (με 4 μόνο δια-φορετικά χρώματα) αποτελεί μέρος μιας γενικότερης κατηγορίας τοπολογικών προ-βλημάτων: του 'χρωματισμού γράφων'.

Η μελέτη των δικτύων γέννησε και τη Θεωρία των 'Έξι βαθμών χωρισμού' (6 degrees of separation), γνωστότερη και ως 

θεωρία της Κεντρικότητας  ή των Γράφων (των γραφημάτων, graph theory), που ανέπτυξε το 1927 ο Ούγγρος συγγραφέας Frigyes Karinthy, σύμφωνα με την οποία, κάθε άνθρωπος θεωρείται ότι απέχει ένα βήμα από κάποιον γνωστό του και δύο βήματα από τους φίλους των γνωστών του. 

Σε ένα άλλο πείραμα που έγινε τη δεκαετία του 60 σε περισσότερα από 100 άτομα, επιλεγ-μένα τυχαία από τις μεσοδυτικές Πολιτείες της Αμερικής, διαπιστώθηκε ότι συνδέονταν όλοι μεταξύ τους με ένα χρηματιστή της Μασαχουσέτης (από ένα φίλο ενός φίλου, ενός άλλου φίλου κ.ο.κ.). Η ανακάλυψη της σύνδεσης όλων αυτών των διαφορετικών προσώπων, απέδειξε πώς ακόμα κι ένα μεγάλο δίκτυο μπορεί να είναι τελικά ένας πολύ 'μικρός κόσμος'.

Από το 2009 όμως όλα δείχνουν να αλλάζουν στην θεωρία αυτή, γιατί δημιουργήθηκε ένα πλάνο δικτύωσης που ονομάζεται Glacir. Αυτό φιλοδοξεί να πλέξει μεταξύ τους όλα τα γνωστά δίκτυα υπολογιστών και κοινωνικής δικτύωσης και να θεμελιώσει ένα παγκόσμιο δίκτυο γνωριμίας, που θα κάνει πράξη τους έξι βαθμούς χωρισμού ή σύνδεσης.

το πείραμα

Ένα συχνό πρόβλημα στην εκτέλεση του πειράματος ήταν ότι ένα μεγάλο ποσοστό παικτών αρνήθηκε να προωθήσει το γράμμα, το οποίο δεν έφτασε έτσι ποτέ. Σε ένα πείραμα πχ δεν έφτασαν 232 από τα 296 γράμματα. Από εκείνα όμως που έφτασαν, με 2-10 βήματα, ο Μ.Ο. ήταν 5,5-6 βήματα.

Στο παιχνίδι του Kevin Bacon αποδεικνύεται ότι, από ένα ηθοποιό του Hollywood, μπορείς να φτάσεις σε οποιονδήποτε άλλον, μέσω άλλων που έπαιξαν κάποτε μαζί σε μια ταινία, με έναν μέσο όρο 2,7 μόλις βημάτων.

Ο κόσμος μας είναι τόσο, μα τόσο μικρός !!!

7 γέφυρες στο Konigsberg της  Πρωσίας (το σημερινό Καλίνιν- γκραντ της Ρωσίας, όπου έχουν  απομείνει μόνον 3), στον ποταμό Πρέγκελ, συνέδεαν τις δυο  νησίδες με τις όχθες του ποταμού.

Οι κάτοικοι του ασχολούνταν για δεκαετίες με έναν γρίφο, που έχει μείνει στην ιστορία ως: 'οι γέφυρες του Κένιγκσμπεργκ'.


ο γρίφος 

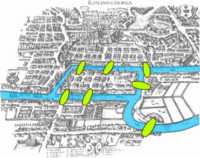Το πρόβλημα ήταν αν μπορούσες να γυρίσεις στο σημείο από όπου ξεκίνησες, περνώντας από όλες τις γέφυρες, από μια μόνο φορά.

Κάποιοι ισχυρίζονταν πως το είχαν καταφέρει, αλλά στην πράξη δεν μπορούσαν να το αποδείξουν.

Το πρόβλημα παρέμενε αναπάντητο.

Ο Ελβετός μαθηματικός Leohnard Euler έλυσε τον γρίφο το 1736 (πα-ρόμοιο με το πρόβλημα της μονο-κοντυλιάς). Απέδειξε ότι δεν έχει  λύση αφού από κάθε κομμάτι ξηράς περνάει  περιττός αριθμός γεφυρών (έπρεπε να είναι άρτιος) σχεδιά-ζοντας την πόλη (σχηματικά, χωρίς λεπτομέρειες, που δεν παίζουν κα-νένα ρόλο) στο χαρτί.

Η λύση του Όϊλερ άνοιξε το δρόμο για την Τοπολογία, που αποτελεί σήμερα κλάδο των Εφαρμοσμένων Μαθηματικών, με πλήθος εφαρμογών.

       

Παρακολουθήστε τη σταδιακή παραμόρφωση της ρεαλιστικής απεικόνισης (αριστερά), μέχρι το τελικό απλουστευμένο διάγραμμα. Με μια έντονα αφαιρετική διαδικασία μπορούμε να αντιστοιχί-σουμε κάθε κομμάτι ξηράς απλά με ένα γράμμα. Πχ Α και D για τα δυο νησάκια και B, C για τις δυο όχθες του ποταμού. Στη συνέχεια παριστάνουμε καθένα γεφυράκι με μια (καμπύλη) γραμμή, που συνδέει δυο κομμάτια ξηράς. Καταλήγουμε σε ένα απλούστατο σχήμα, με τα γράμματα σαν κόμβους-κορυφές (nodes) και τις γέφυρες σαν συνδέσεις-ακμές (edges), χωρίς να καταστρέφεται η βασική δομή του σχήματος.